石英晶体微稳定(QCM)是一种极其敏感的质量平衡,可测量每单位面积的质量质量变化纳米图。该技术的核心是石英光盘。石英是一种压电材料,可以通过通常通过金属电极施加适当的电压来以限定的频率振荡。振荡的频率可以通过添加或移除少量质量在电极表面上而影响。可以实时监测频率的这种变化,以获得有关在电极表面上进行的分子相互作用或反应的有用信息,例如膜生长,氧化,腐蚀/衰减等60岁,在真空下使用QCM和气相,1-2大约40年前,该技术显示在液体介质中也适用。3.
相关的
通过真空或气相的分子吸附通常会产生与电极表面振荡完全耦合的刚性薄膜。因此,薄膜质量的变化与振荡频率的变化是线性相关的,振荡频率是由著名的索尔布雷方程定义的。通过实时监测频率的变化,QCM可以提供有关沉积质量量和沉积(或去除)速度的有用信息。1-2然而,在液体环境中,分子吸附包括通过直接水化/溶剂化和/或在吸附膜内的包封,结合的液体分子作为额外的动态质量贡献。吸附可以产生软的或粘弹性的薄膜,产生的薄膜可能不能完全耦合到振荡晶体上。这可能导致振荡的衰减或能量损失。这类薄膜的质量不能仅靠测量频率的变化来精确测定。频率变化(Δf)和能量损失(测量为耗散变化,ΔD)都需要测量,才能准确地确定粘弹性薄膜的质量变化。此外,通过监测Δf和ΔD,可以获得额外的结构信息(例如,膜中的构象变化、交联和膨胀)。这种技术被称为耗散石英晶体微天平(QCM-D)。4.
QCM-D还提供了吸附膜粘弹性特性的实时信息,如粘度、弹性和密度。该技术在液体中的最大质量灵敏度小于1 ng/cm2..可测得的最大膜厚度从几百纳米变化到几微米,这取决于膜的刚性。QCM-d具有广泛的科学各个领域的应用。188金宝搏app安卓下载Some examples include: kinetics of molecular interactions (e.g., protein-protein interactions), molecule-surface interactions (e.g., affinity of bio-molecules to the binding site of a functionalized surface), buildup of polymer films and their interactions with different constituents of liquid media, effect of surfactants on various coatings, biosensor applications, etc.5-10
理论和仪器
石英:压电谐振器
QCM的操作是基于发生在被称为“偏心”的材料的某些晶体的结晶材料的压电效应,11-12石英属于这类晶体。压电单词来自希腊语“Piezein”,这意味着“按”,以及响应于这些类型材料中的施加压力而产生的电力。压电性被定义为响应于由机械应力引起的机械变形的电力的产生,或者在这种晶体中施加电力的物理变形的产生。当沿着某些晶体取向变形时,法国物理学家皮埃尔和雅克居里在1880年发现了这种效果。11一年后,他们证明了逆转效应也是可能的,即,石英可以在电压的应用时变形。
除了压电之外,石英还具有独特的性能组合,使其成为超敏感装置的理想候选者。它在大自然中发现丰富,并且很容易成长和过程。另外,α-石英,可用作谐振器的石英的相位,热力学稳定高达573°C。
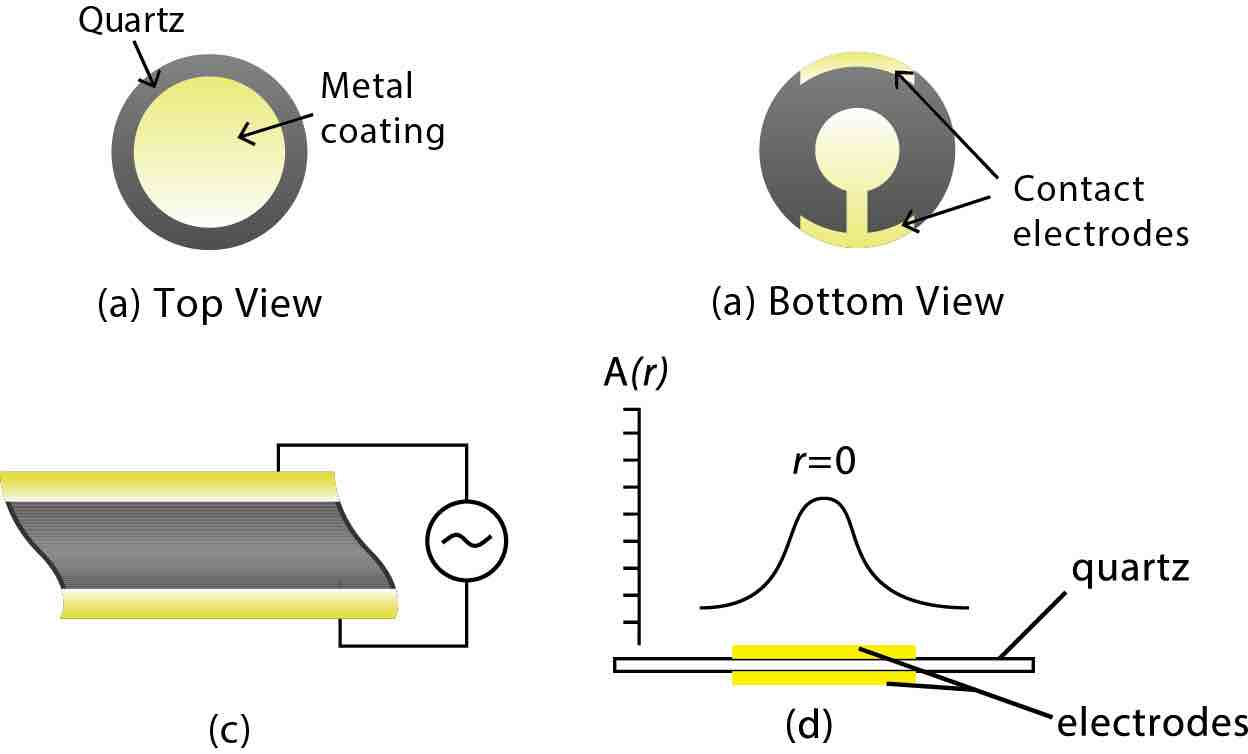
为了制作石英晶体谐振器,从块体石英晶体上切割晶片,切割方向与晶体学轴有关。QCM中使用的石英盘通常使用“at切割”进行加工这提供了纯厚度剪切模式振荡,其中晶体的两个表面以反平行方式移动。13切割后,一对金属电极(通常为金)直接蒸发在石英盘的顶面和底面上(图1)。当相应的交流电作用于石英盘时,石英盘将以其共振频率振荡。共振频率通常为MHz量级,与晶体厚度成反比。普通5 MHz石英晶体的相应厚度约为330µm。
在室温(25℃)中具有良好的稳定性,即最小频率变化(1-3 Hz /°C),设计成具有良好的稳定性。温度对各种角度切口频率的影响是众所周知的和记录的。2,14-16然而,当晶体浸入液体中时,这种接近零温度系数可以增加。剪切模式振荡与液体温度依赖性粘度的耦合可以将温度系数增加到约8Hz /℃的水。因此,对于QCM的高精度测量,需要仔细控制晶体围绕晶体的温度(至<= 0.1°C)或伴随的精确测量。
QCM的质量灵敏度:Sauerbrey方程
在QCMS的频率变化可以与晶体1赫兹或更低的分辨率,在MHz范围中的基本谐振频率来测量。由于它的高稳定性作为谐振器的,石英的晶体成功地掺入,在20世纪初,在各种装置,如电子滤波器,频率控制装置,和超声换能器组件。17-18在Sauerbrey的开创性工作之后,石英晶体作为灵敏质量天平的应用在20世纪50年代末实现。Sauerbrey在1959年证明,振荡石英的频率变化(Δf)可以与它的质量变化(Δm)线性相关
Δm=-C*1/n*Δf(1)
其中n是泛音数,C是一个常数,取决于所用晶体的性质。方程1,通常称为Sauerbrey方程,构成了QCM技术的基本原理。2.在室温下为5MHz的AT切割的石英晶晶,C大约等于17.7 ng /(cm2.·赫兹)。这意味着每厘米增加17.7纳克2.5 MHz石英晶体上的质量变化会导致1 Hz的频率变化。在真空中,5 MHz石英的频率可以轻松测量,精度为0.01 Hz;因此,可以实现纳克级质量的测量。例如,添加面积密度约为25 ng/cm的单层水时的相应频移2.到AT切割石英晶体的表面是大约检测限内1.4赫兹和井。在1963年,华纳和斯托克证明质量变化小至1微克/平方厘米的测量2.这相当于氢单层的0.1%。19
索尔布雷开发方程1假设加入到晶体小质量可以如石英晶体本身的质量的等效变化进行处理。这意味着该方程式是唯一有效的,当附加质量刚性地吸附,没有滑移石英表面上。索尔布雷的发现是在图2中示意性地索尔布雷描绘继续他的QCM的质量传感特性的调查,后来表明,晶体振动被限制为其中电极重叠,如图所示1d的区域。振动的这个区域被称为晶体的活性区域。振动的振幅,A(R),峰在电极的中心中,r = 0,并且逐渐变细以高斯方式朝向电极的边缘(图1D)。石英表面面积的这个差动质量灵敏度构成另一个限制为索尔布雷方程,即,质量必须被均匀地分布在活性区域。
综上所述,Sauerbrey方程在以下三个条件下成立:(i)附加质量相对于晶体本身的质量较小,(ii)附加质量被刚性吸附,(iii)质量均匀分布在晶体的活性区域。该方程已用于并仍在多个行业中用于监测真空或气相下金属沉积的速率和厚度。
在液体介质中运行的QCM的开发是推进其应用的下一步。188金宝搏app安卓下载然而,该任务对早期研究人员提出了几项挑战。直到1980年,Nomura和Hattori表明,在液体介质中完全浸没的石英晶体可以在稳定的频率下振荡。20
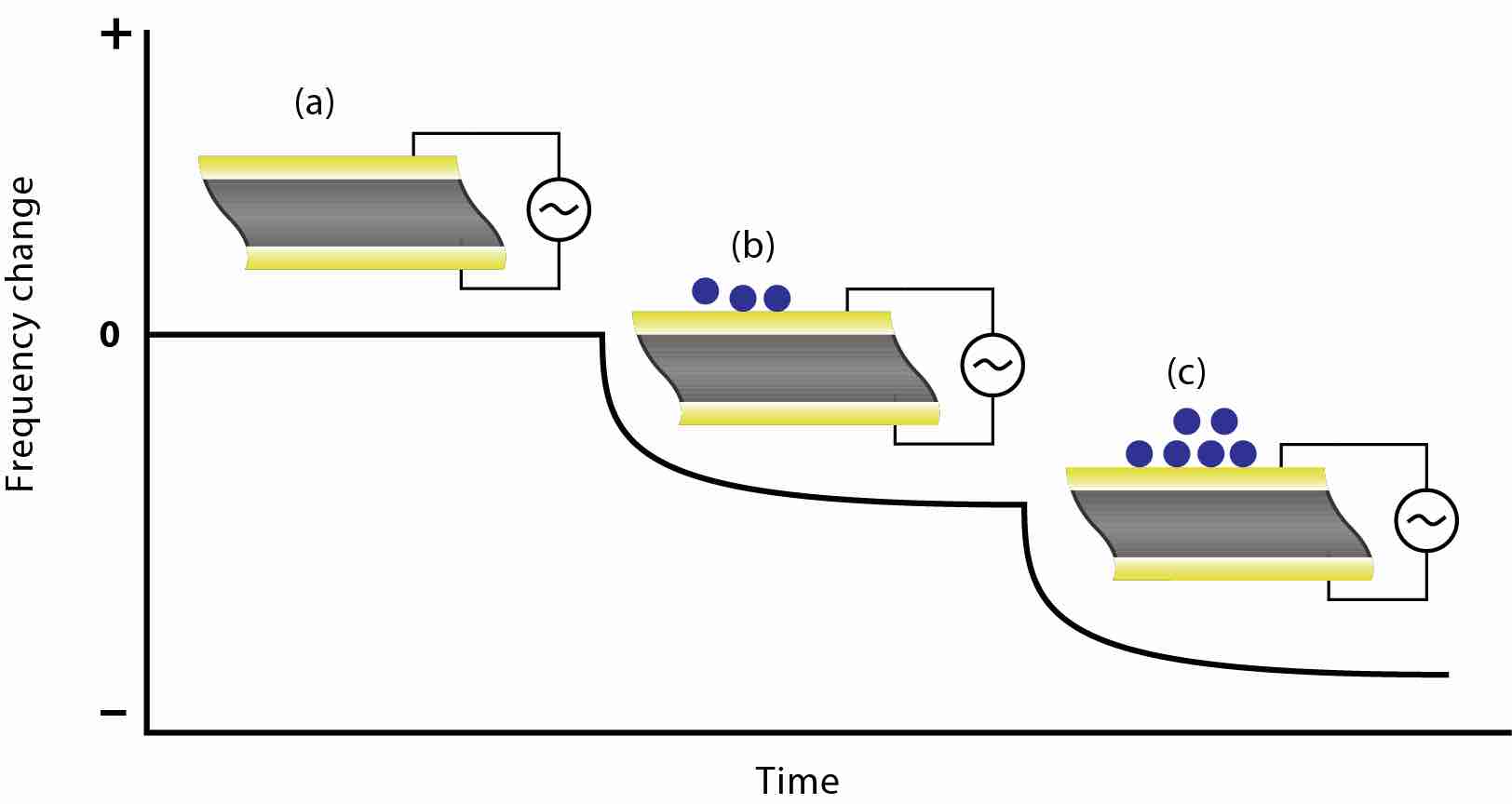
具有能量耗散的石英晶体微天平
随着液体介质QCM的发明,20QCM的188金宝搏app安卓下载应用广泛扩展到生物学、生物技术、聚合物、脂质、蛋白质、电化学、环境研究、纳米颗粒等领域。QCM晶体表面与这些柔性分子系统的相互作用导致软质或粘弹性的形成,违反Sauerbrey条件的薄膜,即束缚质量牢固地附着在晶体表面,没有任何滑移。这种粘弹性薄膜由于柔性质量中的机械损失而导致振荡能量的耗散。由Sauerbrey定义的频率和质量之间的线性关系对于粘弹性薄膜无效。因此,在量化粘弹性质量时,考虑耗散是很重要的。耗散被定义为晶体品质因数Q的倒数,如
D=1/Q=E耗散/ (2π * e存储) (2)
其中E.耗散能量是否在一个周期内耗散,E存储为存储在振荡系统中的能量。
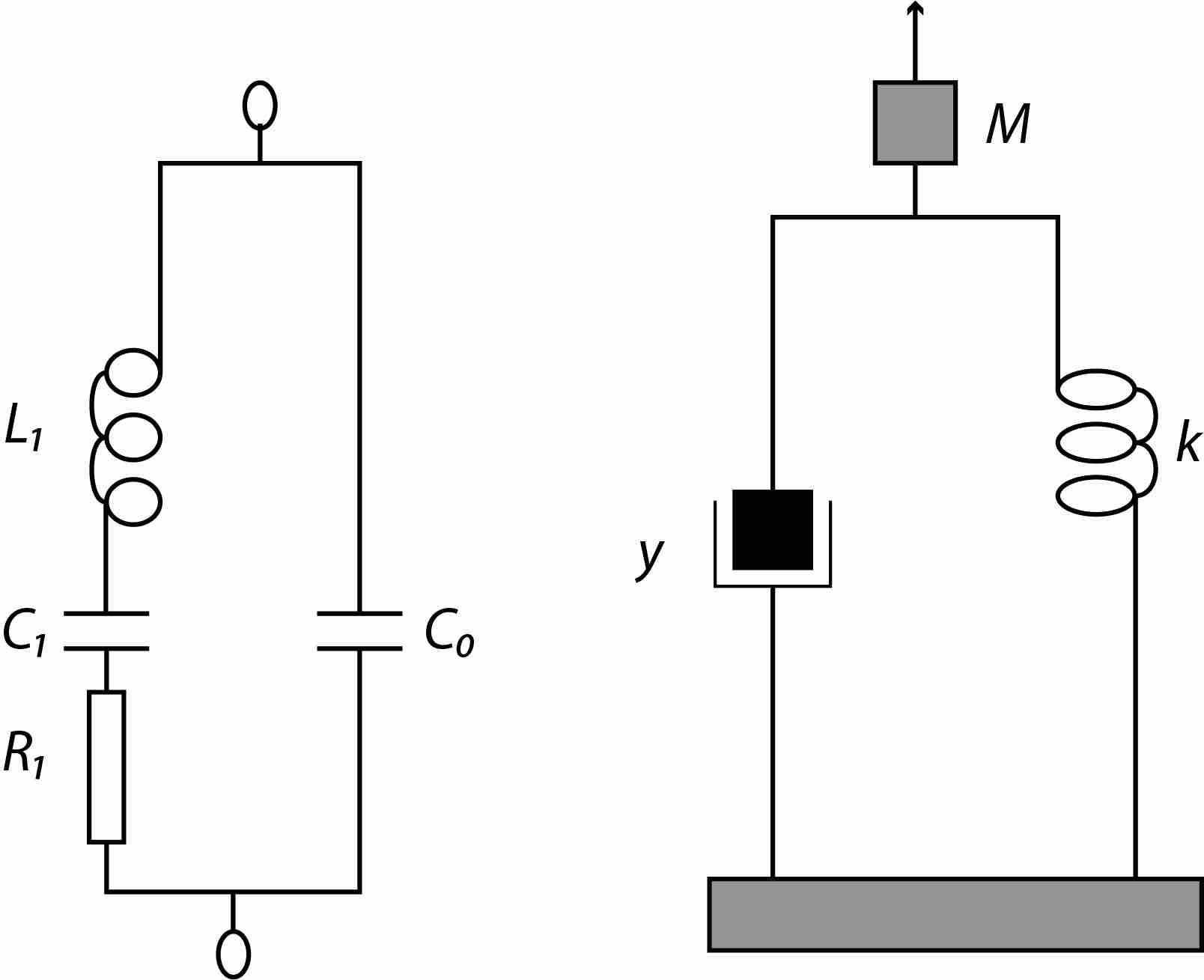
当压电石英晶体共振时,电流和质量同时振荡。因此,石英可以用等效电路(图3a)或机械电路模型(图3b)来表示。21-22该电路模型由电感,L1.,电容,c1.,和阻力,R1.和并联并联电容C0.机械电路模型由质量M和弹簧常数k的弹簧,以及阻尼γ的阻尼器组成。两种模型可以进行如下比较1.代表振荡质量,c1.表示弹性,R1.表示系统中的能量损失。C0为由于晶体表面电极重叠而产生的并联电容。C0纯电气且没有机械模型中的任何表示。
电路模型中的能量耗散可以定义为
d = 1 / q = r1./(2π*f*L)1.)(3)
其中f是指频率。使用电路模型用于测量能量耗散的两个最常见方法是电阻分析(QCM-R)和阻抗分析(QCM-Z)。
在QCM-R中,可以通过将小电阻引入电路并测量电压来测量晶体的电阻。如果分流电容,C0,则谐振晶体等效电路的测量电流将与晶体电阻R成正比1.,即损失的总和。然而,这种方法不提供绝对值,因为1.在这种类型的测量中是未知的。另外,C0如果晶体显着加载,可能无法实现。由于这些原因,电阻方法提供相对结构数据。
QCM-Z是一种更明确的测量能量损失的方法。在这种方法中,可以通过阻抗分析确定晶体等效电路的所有四个元件。23 - 24日该设置包括频率发生器,其向等效电路提供变化的输入频率。电流和相位在频率扫描的每个频率下记录,允许所有四个组件L1.C1., R1.和C0中,待数值拟合。这种方法的限制是等效电路的装配工作,只有当晶体是在稳定状态。晶体需要在每个频率步长被稳定;因此,用这种方法的数据采集速率是相对于其他方法QCM作为慢得多。
第三种越来越受欢迎的方法是QCM-D。在这种方法中,通过施加一个驱动电压,石英晶体在短时间内被激发到其共振频率。然后关闭驱动电压,将晶体上的电压衰减记录为时间的函数。4.晶体上的电压以指数衰减的正弦波的形式衰减
a(t)= a0E.T /τ.SIN(2πft+φ)(4)
如果A幅度,τ是衰减时间常数,f是频率,φ是相位角。衰减时间常数与耗散因子有关
D = 1 / (2πfτ) (5)
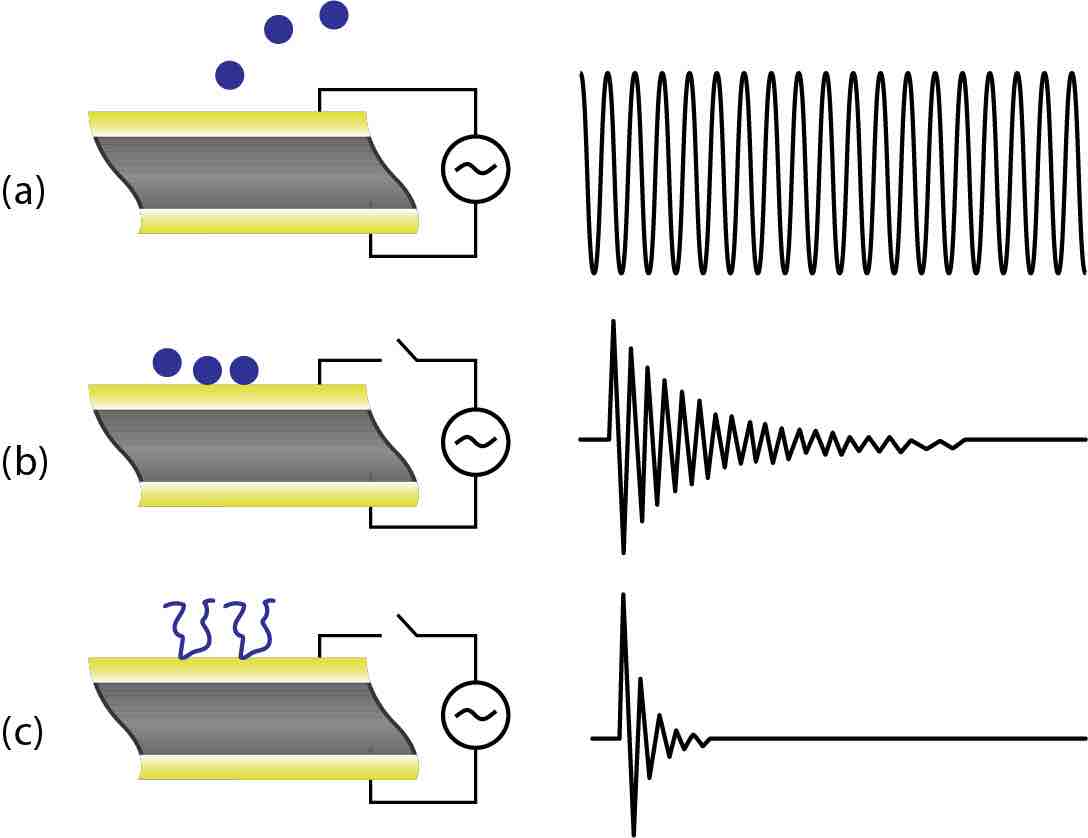
因此,通过数值拟合衰减曲线公式4晶体的频率和耗散可同时获得。衰减时间常数依赖于吸附在晶体表面上的质量的刚性或柔软性。例如,刚性的材料(例如,金属膜)与振荡石英夫妇很好,而且,当驱动电压被关断,振荡需要更长的时间衰变。换句话说,衰减曲线会更长(图4b)。在另一方面,如果吸附质量是软的或粘弹性的,例如蛋白质,脂质,等等,它与振荡石英耦合较差。柔性粘弹性阻尼质量的晶体振荡使其衰减更快,即,衰减曲线会更短(图4c)。
粘弹性模型
阻尼会导致系统中的能量损失。在这种情况下,频率和耗散响应是薄膜特性的函数,如密度、厚度、粘度和剪切模量(弹性)。因此,准确计算粘弹性质量(作为密度和厚度的乘积)需要测量频率和耗散,也可用于获得吸附膜的粘弹性特性。该分析通过将频率和耗散响应拟合到粘弹性(如Voigt,图3b)模型来进行,Voinova等人对此进行了解释。25voigt粘弹性模型包括(粘性)dashpot和(弹性)弹簧并联的布置。图5提供了用散装液中涂覆有粘弹性膜的石英层结构的示意图。
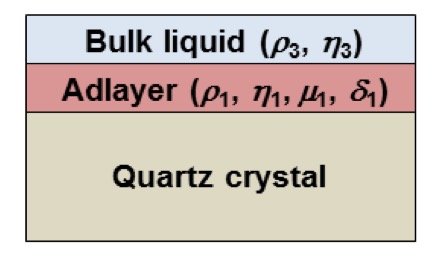
Voinova等人描述,在图5所示的液体介质中吸附粘弹性薄膜时,石英晶体的频率(Δf)和耗散(ΔD)响应可通过以下方式与吸附层的粘弹性特性和液体的体积特性相关:
Δf≈- 1 / (2πρ0δ0){(η3./ δ3.) + δ1.ρ1.ω - 2Δ.1.(η3./ δ3.)2.(η1.ω.2./ μ1.2.+ω.2.η1.2.)} (6)
和
ΔD≈1 / (πfρ0δ0){(η3./ δ3.) + 2δ1.(η3./ δ3.)2.(η1.ω / μ1.2.+ω.2.η1.2.)} (7)
其中ρ0和δ0是石英晶体的密度和厚度,η3.和ρ3.散装液体的粘度和密度,δ3.是散装液中剪力波的粘性穿透深度,ω是振荡的角度频率。ρ1., η1.,µ1.和δ.1.是密度,粘度,剪切吸附层的弹性和厚度,分别。因为有几个未知参数进行识别,Δf的与△D从基本频率的至少两个色彩需要应用此模型。
在石英上粘弹性薄膜的Δf/n和ΔD/n对各种谐波(n)的响应不重叠。相比之下,对于使用Sauerbrey方程的刚性薄膜,这些响应在所有谐波中都倾向于重叠。测量到的Δf和ΔD响应的谐波相关性和耗散变化的大幅度是粘弹性薄膜的主要特征,因此应该使用Voigt模型建模。ΔDn/Δfn比值是判断吸附膜是粘弹性还是刚性的另一个标准。理论上,当耗散大于零时,薄膜应被认为是粘弹性的。然而,一些研究人员提出了某些ΔDn/Δfn的比率作为指导方针,以近似薄膜是粘弹性还是刚性。例如,Cho等人。26表明粘弹性薄膜的ΔDn/Δfn比大于0.1×10-7赫兹-1,而Reviakine等人。27建议当Δdn/Δfn比率远小于4×10时,薄膜可以被认为是僵硬的-7赫兹-1.
设备和操作方法
QCM仪器
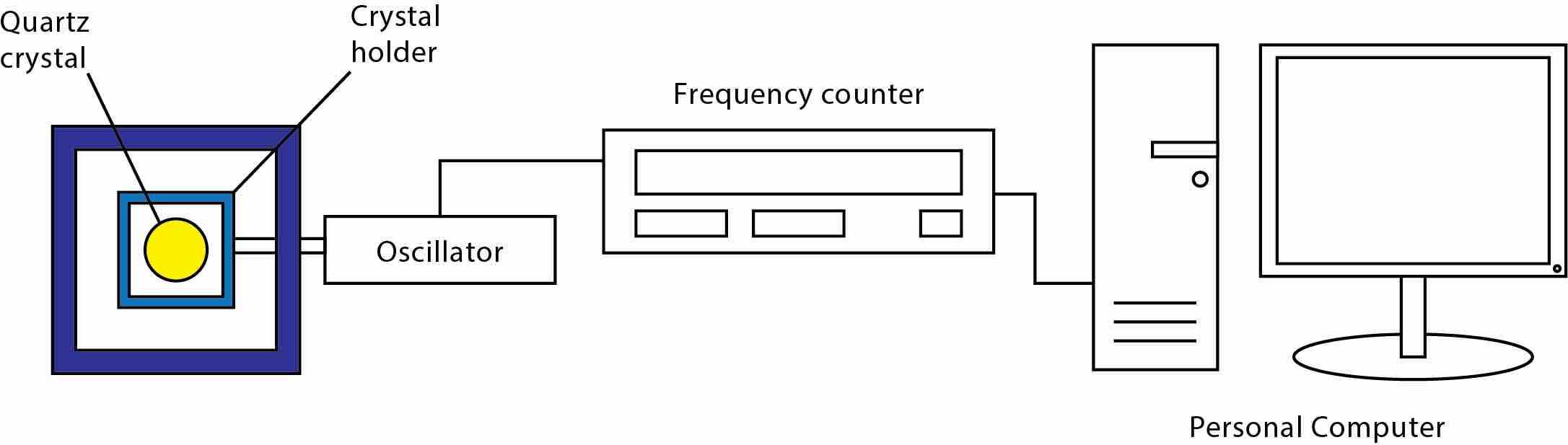
典型的QCM系统包括正面和背面都有电极的石英晶体、固定晶体并提供电气连接的晶体支架、驱动晶体达到其共振频率的振荡器以及读取频率变化和存储过程参数的控制器或监视器(图6)。晶体前部和后部的电极通常为钥匙孔形状(图1),谐振器的中心可能比边缘厚。这种电极设计允许QCM仅在电极沉积的中心区域振荡。28由于晶体振荡而产生的运动波聚焦在石英晶晶的中心,这使得更容易在边缘处安装晶体而不会过度抑制振荡(图1D)。
由于振荡频率稳定性受温度变化的影响,因此石英晶体保持器通常被放置在封闭的温控室中。腔室可定制用于空气/真空或液体介质中的测量。QCM的基本组件相对便宜,因此可以在内部组装。当今商业QCM仪器中存在的许多发展和特征在实验室中开创了具有定制仪器的实验室,以满足特定的研究需求,例如使用内部参考晶体来将液体环境与薄膜样品的影响分离。29 - 30日
今天,尽管定制的QCM仍然很受欢迎,可以根据特定的实验进行定制,但市场上有几种商用QCM,每种QCM都有不同的仪器规格。一些QCM仅在真空或气体中工作,其中沉积的薄膜薄且坚硬,通常使用Sauerbrey方程监测薄膜厚度。随着薄膜厚度的增加,粘弹性效应开始发挥作用,并会影响晶体的共振特性。
QCM-D仪器
对于在液体介质中操作的qcm,主要由液体本身的密度和粘度驱动,粘弹性效应的贡献更大。因此,采取了额外的措施来克服基于液体的qcm的大阻尼的后果。QCM-D就是这样一种近年来越来越受欢迎的技术。QCM-D能够测量能量损失,在短暂激发石英晶体到其共振频率并关闭驱动电压(如上所述和图4所示)后,记录振荡衰减曲线。衰减曲线(即,自由振荡晶体的输出电压振幅随时间的函数)是通过将样品晶体的谐振频率(f0)与参考频率(fR)混合,然后用低通带滤波器对其进行滤波得到的。f0和fR之间的差给出了输出频率,在方程4和5中表示为f。
在毫秒秒的时间内发生了石英晶体和旋转曲线的录音和拟合的整个激励过程。因此,利用QCM-D方法可以实现实时数据采集。QCM-D还使数据采集在晶体基本谐振频率的多个overton处。这些参数通过各种建模理论允许分析实验数据,以获得包括吸附质量,厚度,密度,剪切弹性(也有时称为剪切模量),粘度和动力学的信息的信息。25日,31-32由于QCM-D的快速数据采集,可以实时表征和动力学分析晶体表面发生的分子相互作用(吸附、反应、解吸等)。
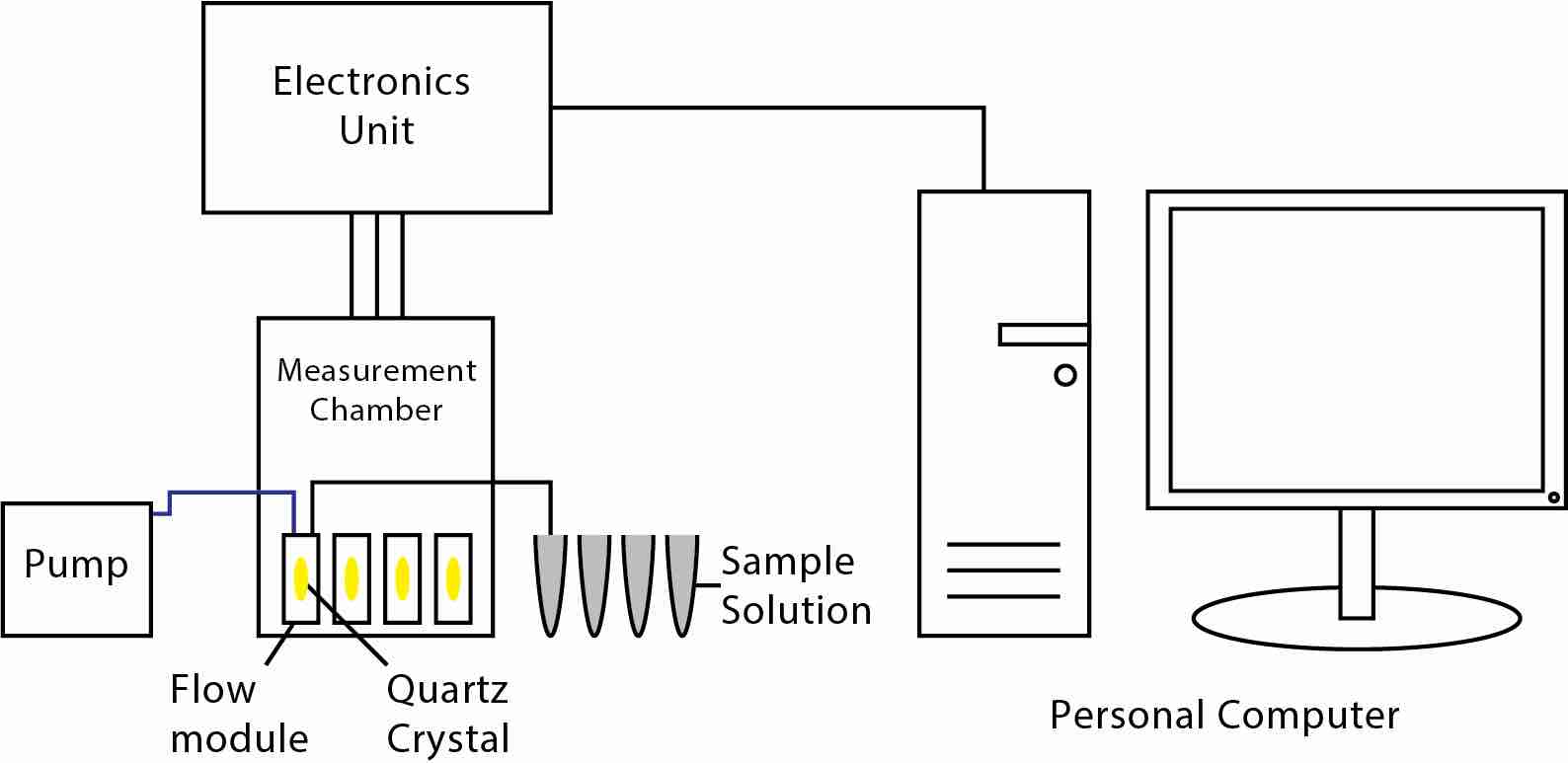
基本的QCM-D仪器包括一个石英晶体,其中电极沉积在前端和背面,一个流量模块,其保持石英晶晶体,使液体介质能够穿过晶体的顶面,泵流动样品溶液,在设定温度上安装并保持流量模块的温控室,以及通过施加适当的电压和记录频率和耗散变化来驱动晶体的电子单元。其中一个最常见的QCM-D仪器型号包含四个流量模块(参见图7),每个流量模块均保持石英晶晶晶体,并在同一时间同时同时测量多达四个QCM-D传感器的频率和耗散变化。
1.Lu C.和A.W. Czanderna .压电石英188金宝搏app安卓下载晶体微天平的应用,Elsevier科学出版社B.V.,阿姆斯特丹,NL, 1984。
2. G. Sauerbrey,Verwendung von SchwingquarzenZurwägungDünnerSchichtenund ZurMikrowägung,ZeitschriftFürspeyik,155(2),206-222(1959)。
3. T.野村和A.峰村,在水溶液中的压电石英晶体的行为与该应用程序氰化物分钟量,日本化学揩拭,10,1621年至1625年(1980年)的确定。
4.罗达尔和卡西姆,石英晶体微天平的谐振频率和绝对耗散因子的测量方法,科学仪器评论,67(9),3238-3241(1996)。
5. M.A. Cooper和V.T.Singleton,对2001至2005年石英晶微观生物传感器文献的调查:声学物理学在分分配分析的应用,分子识别杂志,20(3),154-184(2007)。188金宝搏app安卓下载
6. M.C.迪克森,石英晶微观测量耗散监测:实现生物材料的实时表征和它们的相互作用,生物分子技术杂志,19(3),151(2008)。
7.P.L.Konash和G.J.Bastiaans,压电晶体作为液相色谱检测器,分析化学,52(12),1929-1931(1980)。
8.Liu Y., A. Jaiswal, et al., Surface Plasmon Resonance and Quartz Crystal Microbalance Methods for Detection Molecular Interactions, in chemistry sensors: Principles, Strategies, an188金宝搏app安卓下载d application . (sci)Wang B. and Anslyn E.V., (Eds), 2011。
9A.Janshoff,H.J.Galla和C.Steinem,《作为生物传感器的压电质量传感装置-光学生物传感器的替代品》,Angewandte Chemie国际版
10.B. Becker和M.A. Cooper, 2006-2009年石英晶体微天平生物传感器文献综述,分子识别学报,24(5),754-787(2011)。
11.W.G.Cady,《压电:机电现象的理论和应用导论》,多佛出版社,美国纽约,1964年。188金宝搏app安卓下载
12.M.D. Ward和d.a Buttry,压电换能器的原位界面质量检测,科学,249(4972),1000-1007(1990)。
13.F. Lack, G. Willard,和I. Fair,石英晶体电路元件的一些改进,Bell系统技术期刊,13(3),453-463(1934)。
14《理解压电石英晶体》,射频设计,23,50-59(2000)。
15.“石英晶体微天平理论和校准。”http://www.thinksrs.com(访问4月)。
16.“RQCM-研究石英晶体微天平:操作和服务手册”,Inficon;美国纽约州东锡拉丘兹,2007年。
17《美国石英晶体工业史》,第35届年度频率控制研讨会论文集,3-12(1981)。
18. D. D. Sullivan,NIST的时间和频率测量:前100年,IEEE国际频率控制研讨会和PDA展览会,4-17(2001)。
19.A.W.华纳和C.D.斯托克布里奇,石英谐振器;温度变化引起的瞬时频率偏移的减少,应用物理学报,34(2),437-438(1963)。
20.野村和服部,用压电探测器测定溶液中氰化物的微摩尔浓度,分析化学学报,115,323-326(1980)。
21. D.A.Buttry和M.D.Ward,电极表面的界面过程测量电化学石英晶体微稳定,化学品评论,92(6),1355-1379(1992)。
22.J. Janata,化学传感器原理,静压出版社,美国,1989。
23. A. Janshoff,J.韦格纳。,等人,上剪切波谐振器中培养的上皮细胞单层,欧洲生物物理杂志,25(2),93-103(1996)的双模式阻抗分析。
24J.Wegener,J.Seebach等人,《剪切波谐振器对哺乳动物细胞附着的复合响应分析》,生物物理杂志,78(6),2821-2833(2000)。
25M.V.Voinova,M.Rodahl等人,《流体-固体界面上层状聚合物薄膜的粘弹性声学响应:连续介质力学方法》,Physica Scripta,59391-396(1999)。
26.N.-J。赵志刚,等,石英晶体微平衡与耗散监测支持的脂质双层基质,自然学报,5(6),1096-1106(2010)。
27I.Reviakine,D.Johannsmann和R.P.Richter,《听你看不见的,看你听到的:从溶剂化界面解释石英晶体微天平数据》,分析化学,838838-8848(2011)。
28. v.E.底部,石英水晶单元设计介绍,van nostrand Reinhold,纽约,美国,1982。
29. S.Bruckenstein,M. Michalski等。,双石英晶体微矛盾振荡器电路。最小化液体粘度,密度和温度,分析化学,66(11),1847-1852(1994)引起的效果。
30. G.C.Dunham,N.H.Benson等人。,双石英晶体微稳定,分析化学,67(2),267-272(1995)。
31.M.Rodahl,F.Hök等人,《生物分子吸附和细胞粘附的同时频率和耗散因子QCM测量》,法拉第讨论,107229-246(1997)。
32. A. Domack,O. Prucker等人,用石英晶体谐振器探测的聚合物刷的溶胀,物理评论E,56(1),680(1997)。