表面张力，表面自由能和润湿性

表面自由能告诉我们什么?

固体表面的表面自由能(SFE)可以告诉你很多关于不同液体将如何与所述表面相互作用的信息。在我们的表面自由能技术页，我们讨论了如何从接触角测量中计算固体的SFE，使用几个模型，包括常用的Owens-Wendt-Rabel-Kaelble模型。但一旦你测量了SFE，下一个逻辑问题是“我能用这些信息做什么?”事实上，OWRK模型是一种基于SFE和液体表面张力预测润湿性和粘附性的强大工具，可以帮助指导您的研究和开发。在这一页中，我们将介绍湿信封作为一个方便的可视化工具，并解释SFE、表面张力和接触角之间的关系。

欧文斯-温特-拉贝尔-卡贝尔模型

在这些分析中，通常使用OWRK模型，其中液体表面张力，γ_LV，是色散分量(γ)的和^D_LV如伦敦色散力)和极分量(γ^P_LV如氢键)使γ_LV=γ^D_LV+γ^P_LV．同样，固体SFE， γ_SV，是色散分量和极性分量的和，如γ_SV=γ^D_SV+γ^P_SV．然后用OWRK方程描述液体表面张力、固体SFE和液固接触角之间的关系:

（1）

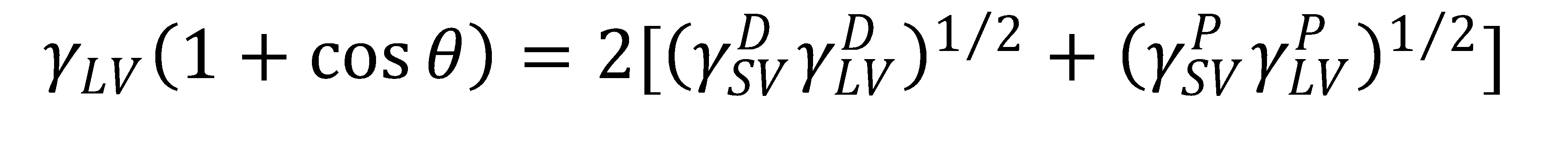
θ是液体和固体之间的接触角。在OWRK模型中做了一些重要的假设:液体是纯的，固体是光滑的，化学上是均匀的，液体和固体之间没有化学反应。没有一个真实的系统能够完全满足所有这些假设，但尽管如此，OWRK模型是一个强大的模型，被广泛用于工业和学术界，以指导材料的选择。

什么是湿信封?

液体表面张力、固体表面自由能和液滴在表面的接触角都是相关的。湿润的外壳帮助我们可视化这些关系，可以帮助我们更好地理解我们的系统和选择材料。

图1显示了含γ的理论固体的润湿包络线图^D_SV= 30 mN/m和γ^P_SV= 10 mN / m。这意味着极值比是γ^P_LV/γ_LV= 0.25，弥散比为γ^D_LV⁄γ_LV= 0.75。在这两幅图中，实色线是夹角θ固定的等值线，也就是说，如果沿着任意一条线运动，θ将保持不变。在图1A中，纵轴表示随γ的变化^P_LV，横轴表示随γ变化^D_LV．在图1B中，横轴表示总表面张力随γ的变化_LV代替。这两幅图代表了具有相同等值线的相同系统。图1A的风格在文献中更常见，但如果你更喜欢用γ来表示润湿性，图1B可能更方便_LV和γ^P_LV．

当解释液体表面张力的极性和色散分量的变化如何影响θ时，这些图特别有用。例如，在图1B中，考虑总表面张力为γ的液体_LV= 40 mN/m和γ^P_LV= 0 mN/m(表示γ^D_LV= 40 mN / m)。接触角开始接近40°，如黄色等值线所示。现在增加γ^P_LV通过在图中垂直移动，你会注意到θ开始下降。在γ^P_LV=10 mN/m时，液体表面张力的极性和色散比与固体的极性和色散比相匹配，用黑色虚线表示。在这一点上，对于给定的γ， θ最小_LV，如果我们继续增加γ^P_LV超过10mn /m时，θ又开始增加。

使用这些润湿信封，两个关键的概念，有关表面张力如何影响接触角的可视化。首先，对于给定的γ_LV当液体表面张力的极性和色散比与固体表面张力的色散比相匹配时，接触角最小。我们可以通过图1中乙二醇(γ)的坐标看出这一点_LV= 48 mN/m)和二碘甲烷(γ_LV= 50.8 mN / m)。两种液体的总表面张力相似，但图中显示二碘甲烷的接触角在60°左右，而乙二醇的接触角略低于40°。这是因为乙二醇的极性和分散比与固体SFE的极性和分散比更匹配。

第二个概念是，如果γ_LV如果足够低，极性和色散比可能不会有太大区别。取图1中表示乙醇带有γ的点_LV= 22.4 mN / m。润湿包络表明，θ = 0°或存在完美润湿，如果改变极性和色散比，仅仅因为γ，仍然存在完美润湿_LV是如此之低。

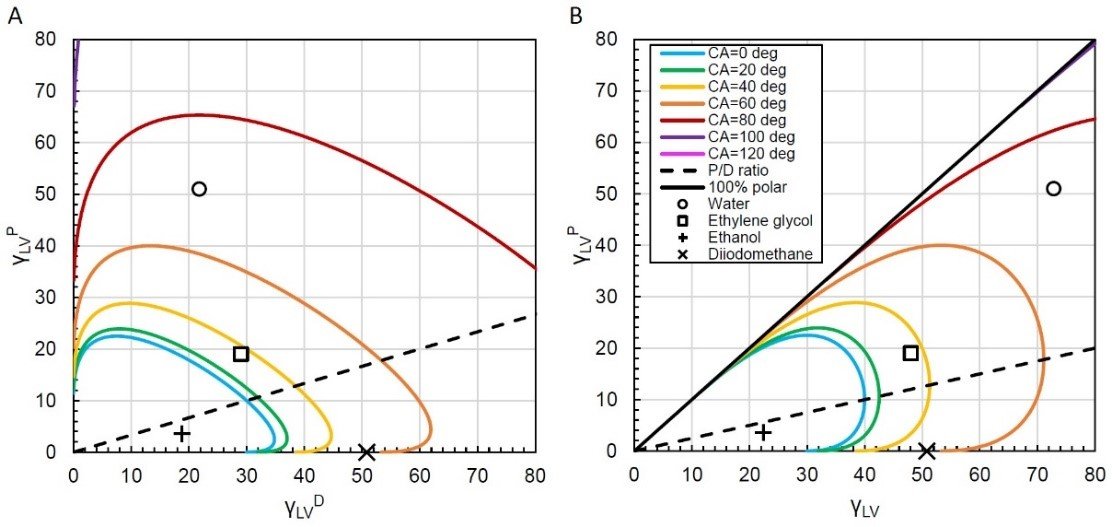图1 -含γ的固体的润湿包络图^D _SV=30 mN/m和γ^P _SV= 10 mN / m。在(A)水平轴是弥散表面张力分量γ^D _LV， (B)横轴为总表面张力γ_LV．点代表水、乙二醇、乙醇和二碘甲烷。

我们如何利用表面自由能和润湿信封来了解润湿性?

利用我们的润湿包膜知识和表面张力、表面自由能和接触角之间的关系，我们可以智能地处理各种研究和开发问题。无论您的目标是增加润湿性(降低θ)还是降低润湿性(增加θ)，我们的选择是修改固体或修改液体。

如果我们的计划是修改液体以增加润湿性，或目标应该包括(a)得到极比γ^P_LV⁄γ_LV和弥散比γ^D_LV⁄γ_LV更接近固体，和/或(b)减少总表面张力。在前一节中，我们研究了改变液体性质如何影响特定固体衬底上的接触角。

在许多情况下，液体可能是固定的或很难充分地修饰，而操纵固体的性质则比较容易。这方面的一个很好的例子是涉及聚丙烯等聚合物涂层的应用。188金宝搏app安卓下载聚丙烯是一种应用广泛的聚合物，因为它具有良好的耐化学性、加工性和相对较低的成本，但它是天然疏水的，很难被许多液体润湿。未经处理的聚丙烯的润湿包膜如图2A所示，由于其低的SFE和主要的分散性，从这一可视化可以清楚地看到，很少有液体能很好地润湿材料。即使是表面张力较低的乙醇，与聚丙烯的接触角也非零。

然而，聚丙烯的SFE易于操纵等离子体处理，并在应用注意事项“增强润湿性等离子体处理聚丙烯我们证明了有一个最佳的处理时间，以获得最佳的SFE润湿性能。通过图2b中经过5 s空气等离子体处理后的聚丙烯润湿包络图，可以看到总SFE增加了，但极性组分也显著增加，为具有显著极性组分的液体(如水和乙二醇)提供了更好的润湿性。这使得像乙二醇这样的液体在未经处理的聚丙烯上的接触角从略低于80°(图2b)降低到等离子处理聚丙烯上的<40°(分别图2a和B)。

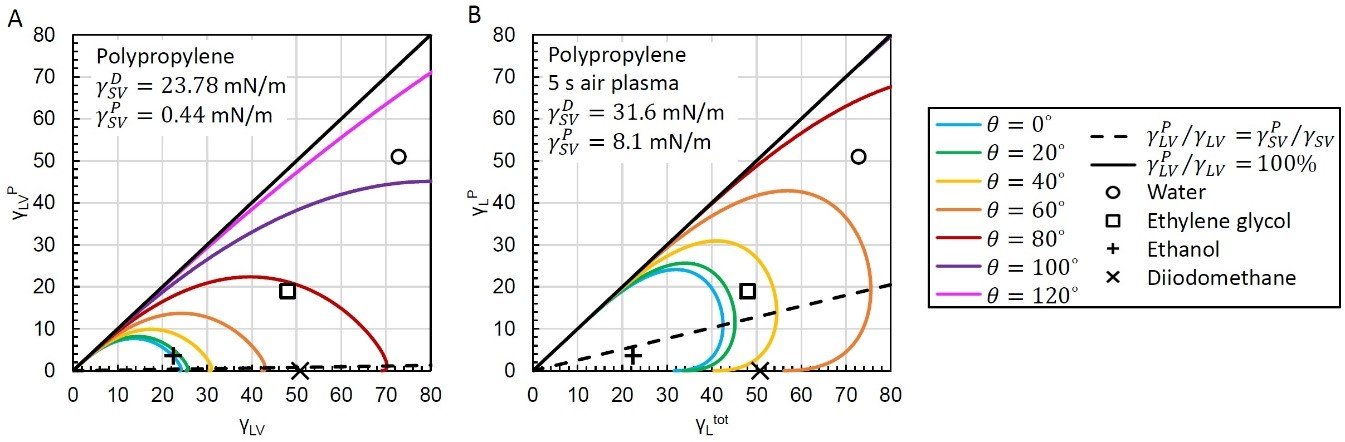图2 - (A)未经处理的聚丙烯和(B)经过5s空气等离子体处理的聚丙烯的湿包膜。所有的SFE测量都是在纳米科学的分析使用一个伸缩光学张力计．

如何制作湿润信封图?

润湿信封图是非常有用的工具，它们不需要比微软Excel更复杂的东西来创建。我们从OWRK方程开始，用极坐标重新写一下。

图3 -用于绘制润湿包络图的极坐标系统。

在图3的极坐标系统中，γ^D_LV和γ^P_LV图1A中的坐标用角度Φ和半径R来描述，其中:

(2)γ^D = R cosΦ,

(3)γ^P = R罪Φ

在OWRK模型中，这意味着在这个极坐标系统中的总表面张力为γ_LV=R cos⁡ϕ+R sin⁡ϕ。使用这些关系，只需将它们插入OWRK方程，

（4)

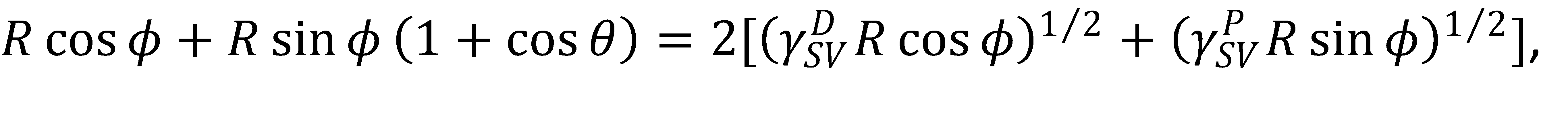
然后求出半径R，

（5）

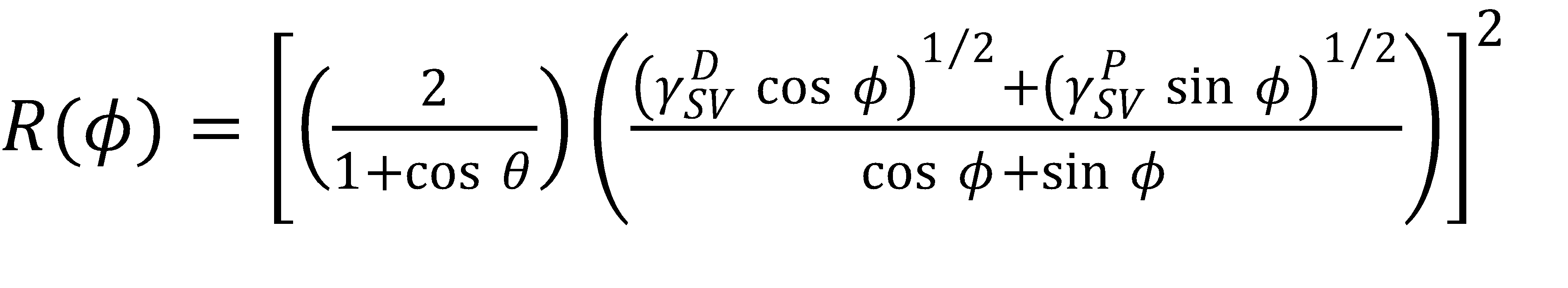
对于给定的θ， γ^D_SV和γ^P_SV，并可直接计算出0^ tong≤ϕ≤90^ tong范围内的R(ϕ)，然后只需使用公式(2)和(3)来确定γ就可以了^D_LV和γ^P_LV．这在能级θ处产生一条等值线。然后，通过对多个θ重复这个过程，可以构建一个润湿包络等高线图来可视化系统，并发挥不同的液体或固体性质。

符号及其定义列表

• γ_LV:总液蒸汽压，其中γ_LV=γ^P_LV+γ^D_LV
• γ^P_LV:汽液表面张力的极性分量
• γ^D_LV:液-蒸汽表面张力的分散组分
• γ_SV:固体-蒸气表面总自由能，其中γ_SV=γ^P_SV+γ^D_SV
• γ^P_SV:固汽表面自由能的极性分量
• γ^D_SV:固气表面自由能的分散组分
• ϕ:液滴在固体表面的接触agnel
• Φ:用于绘制湿润包络图的极坐标系统中的角坐标
• R:用于绘制润湿包络图的极坐标系统中的径向坐标

润湿信封计算器

下面是一个excel电子表格，你可以下载并使用它来计算和可视化湿信封: